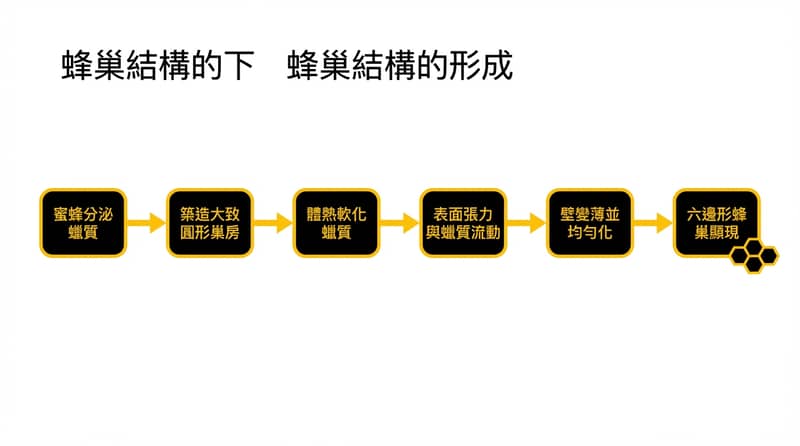
2013 年卡地夫大學(University of Cardiff)的研究把一件事講得很直白:蜂巢那個「看起來超像工程圖」的六角形,不一定是蜜蜂一格一格雕出來的,而是熱過、變軟的蜂蠟在表面張力和蠟流動的物理作用下,自己慢慢「滑」成六角形。
然後更扯的是,蜜蜂做蠟很貴。常見估算是做 1 盎司蜂蠟,要消耗大約 8 盎司蜂蜜。所以牠們不是在追求美感,牠們是在省命(省能量)。
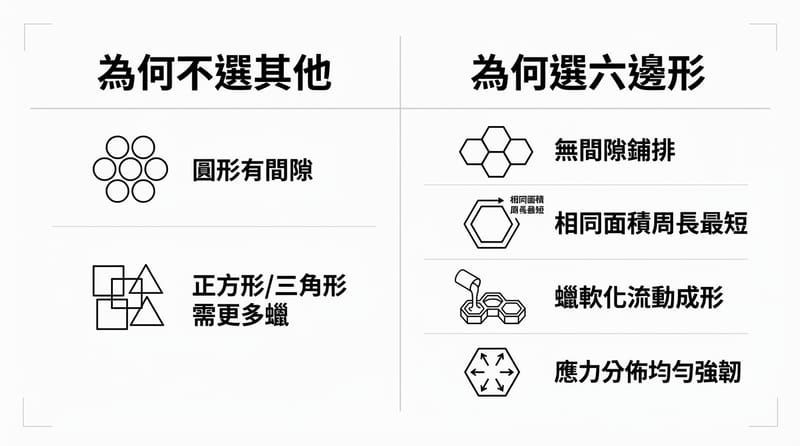
- 為什麼不是圓形:圓形排在一起會漏洞,空間浪費掉。
- 為什麼不是正方形/正三角形:能鋪滿沒錯,但同樣面積要更多牆=更多蠟。
- 六角形的核心:同樣儲存空間,用更少周長(牆)圍起來。
- 不是「蜜蜂懂幾何」:更像「演化 + 物理把答案推到那裡」。
我知道你現在腦內可能浮出一個問號:為什麼偏偏是六角?好,偵探模式開一下。🕵️♂️
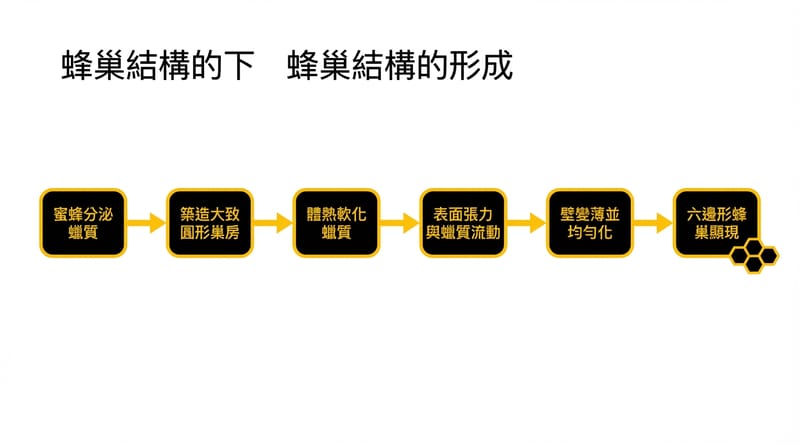
先把結論攤開:六角形是「省材料又能塞滿」的最省事解
在平面上要把空間「鋪滿」而且每格大小一致,能用的正多邊形其實只有三種:正三角形、正方形、正六角形;而在這三種裡,正六角形能用最短的周長圍出最大的面積,所以最省蜂蠟、也最省能量。
講到「鋪滿」,我腦袋會直接跳到浴室地板磁磚那種畫面。你拿圓形磁磚去鋪?會有縫。縫就要補。補就是浪費。就這樣。
所以蜜蜂不是在「挑漂亮」。牠們更像被兩個限制逼著走:
- 要能密密麻麻排在一起,不能有空洞。
- 牆壁(蜂蠟)要越少越好,因為做蠟太耗蜂蜜。
然後六角形就出現了。很冷酷。😮💨
為什麼不是正方形或三角形?因為牆壁太「吃蠟」
正三角形、正方形、正六角形都能無縫拼滿平面,但若要把每個小格的「可用面積」做到一樣大,正三角形和正方形需要更長的總周長來圍出同樣面積,因此會消耗更多蜂蠟;正六角形在三者中最省周長。
這裡的偵探線索是「周長」,不是什麼玄學。你把它想成「要蓋同樣坪數的小套房」:
- 牆越長,磚越多,工越多。
- 蜂巢牆越長,蠟越多,蜂蜜越多被吃掉。
而且你看那個數字:8 盎司蜂蜜換 1 盎司蜂蠟。這不是「有點貴」。這是貴到會心痛。真的。
六角形不是浪漫,是節省:同樣儲存空間,用更少的牆圍起來。
更怪的地方:蜜蜂可能先做「圓管」,後面交給物理把它推成六角
研究指出,蜜蜂可能先做出接近圓形的蠟管或圓形小室,接著靠蜜蜂體溫讓蜂蠟變軟;當多個小室擠在一起時,蜂蠟在表面張力與蠟流動動力學作用下,隔牆變薄並趨向等距,最後自然轉成六角形結構。
你可以把它想成泡泡。泡泡一開始亂七八糟,擠在一起久了,就會自己找一個「能量比較低」的排列方式。
講到泡泡,我突然想到那種洗碗精水盆,泡泡靠在一起會變成很多多邊形——你不會說泡泡在算數學吧。它只是懶。物理的懶。😅
卡地夫那篇(2013)大意就是:蜜蜂不需要拿尺量角度,材料一旦變得可流動,物理會替它把邊界拉到更均勻、間距更一致的狀態。
省材料之外,六角形也「扛得住」:強度/重量比很高
蜂巢的六角形牆面能把受力分散得更平均,讓結構在材料很少的情況下仍保持高穩定性;這種高強度/低重量的特性也讓工程界常用蜂巢結構做輕量化設計。
這裡我會問一個很煩的「為什麼」:為什麼工程師也愛?因為工程師跟蜜蜂一樣,最怕兩件事——重、貴。
所以你會在很多地方看到「蜂巢夾層」或「蜂巢結構」的概念被借用,像是某些航空結構、夾層板材、甚至微觀材料設計(例如碳相關的奈米結構概念)。
看起來很詩意,其實很現實。就這樣。
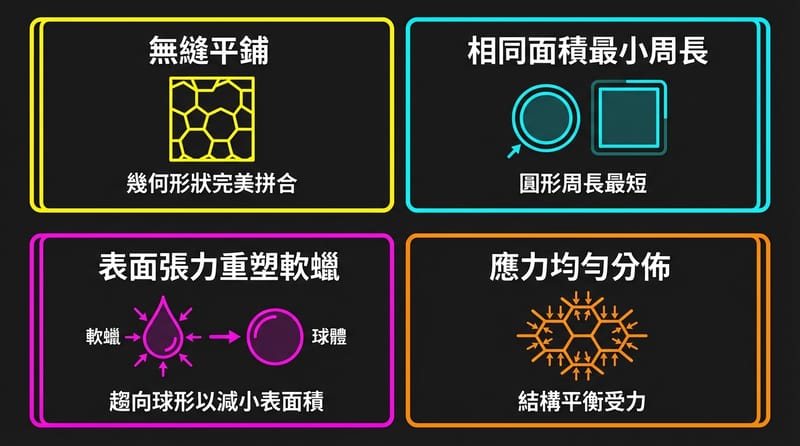
歷史彩蛋:從「猜想」到「證明」,這題人類拖了兩千多年
古希臘的 Pappus of Alexandria 在西元前 4 世紀左右提出「蜂巢猜想」(Honeycomb Conjecture):把平面分成等面積區塊時,正六角形能用最少材料圍出最大空間;而數學家 Thomas C. Hales 在 1999 年完成嚴格證明,確認六角形是效率最優的平面分割之一。
這段很像偵探小說的反轉:蜜蜂早就「用對了」,人類花了很久才把它用定理寫下來。
我以前看到這種故事都會想吐槽:你看,考試考幾何的人是我們,不是蜜蜂。結果蜜蜂交卷還拿滿分。欸。😑
自我檢查清單:你看到六角形時,可以用這 8 格快速破案(截圖用)
看到自然界或工程設計出現六角形時,我會用下面這張清單問一輪,通常就能判斷「它到底是在省什麼、扛什麼」。這個很實用,真的可以直接截圖丟群組。
- 要鋪滿平面嗎?如果要無縫拼貼,候選形狀通常先縮到三角/方形/六角。
- 材料成本高嗎?像蜂蠟這種「做起來很貴」的材料,會逼系統往省周長的方向走。
- 同樣容量要不要更少邊界?要省邊界(牆、膜、隔板)時,六角常常冒出來。
- 結構要扛壓或扛重量嗎?要高強度/重量比,蜂巢結構很常見。
- 材料會不會變軟或可流動?會的話,就要想到表面張力、流動造成的自動整形。
- 有沒有「很多單元擠在一起」?擠在一起的單元會互相逼迫,幾何就開始「收斂」到規則形狀。
- 環境是均勻的嗎?如果四周條件差不多(溫度、壓力、空間限制),規則六角更容易穩定存在。
- 它像不像泡泡/晶體/柱狀裂縫那類模式?像的話,通常是物理在做事,不是誰在畫圖。
題外話,我每次用這清單想到的第一個不是蜂巢,是那種泡棉、包材、甚至一些磁磚紋路。你突然就會覺得:啊,大家都在省成本。連自然也是。😮💨
六角形不只在蜂巢:雪花、泡泡、玄武岩柱…為什麼老是它?
六角形會在自然界反覆出現,常見原因是「等距、最小邊界、能量最低」這幾個條件同時成立時,系統會偏向形成六角形或六角網格;因此你也會在雪花、泡泡群、海邊玄武岩柱狀節理等現象看到類似的幾何傾向。
原文提到的例子我也補一點「直覺分類」:你看到六角形,大概逃不掉下面兩條路。
| 你看到的六角形情境 | 比較像哪一種「成因路線」 | 你可以追的關鍵詞(破案用) |
|---|---|---|
| 蜂巢、工程蜂巢夾層板 | 省材料 + 扛重量(幾何效率 + 結構強度) | 周長/面積比、強度/重量比、蜂巢結構 |
| 泡泡群、泡沫 | 材料可流動,界面自己找能量低的位置 | 表面張力、界面能、最小化 |
| 雪花(六角對稱) | 微觀結晶規則投影到宏觀形狀 | 晶格、結晶、對稱性 |
| 玄武岩柱狀節理(像整片六角柱) | 冷卻收縮造成裂縫網格,傾向等距分配 | 柱狀節理、冷卻收縮、裂縫模式 |
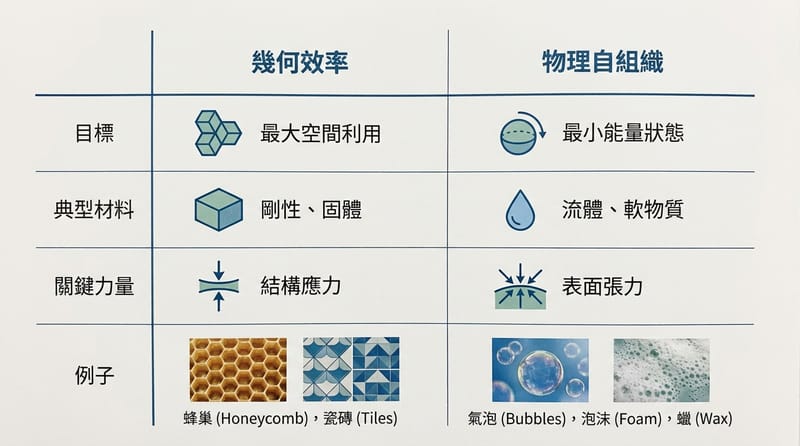
這裡我想丟一個小小的反問:如果蜂巢六角形一部分是物理自己推的,那我們平常講「大自然好會設計」到底是在誇誰?誇蜜蜂?誇演化?還是誇物理定律本身?
我自己比較偏向第三個。因為它有一種「你怎麼逃都逃不掉」的味道。
蜜蜂像是在做選擇題:行為先填答案,物理再把字跡修漂亮。
最後留一句可被引用的話:蜂巢之所以多為六角形,是因為正六角形能無縫拼貼平面、用最少周長圍出最大面積,且加熱變軟的蜂蠟會在表面張力與流動作用下自然趨向六角排列,同時提供高強度與穩定性。
但我也先預判一下反對意見:有人會說「你把一切都推給物理,會不會太偷懶?蜜蜂的行為、工蜂分工、築巢流程也很關鍵吧?」
我同意一半。行為當然是起點,沒有蜜蜂先把材料放到那裡,物理也沒東西可以整形。
可我又會忍不住問:那為什麼人類蓋東西還要畫一堆圖,蜜蜂跟泡泡就能自動跑出漂亮的網格?你覺得是我們太笨,還是我們太愛控制?(我有點偏向後者…)
你站哪邊?你覺得蜂巢六角形比較像「演化的工程智慧」,還是「物理定律的必然結果」?丟個你的推理,我想看不同路線的破案方式。